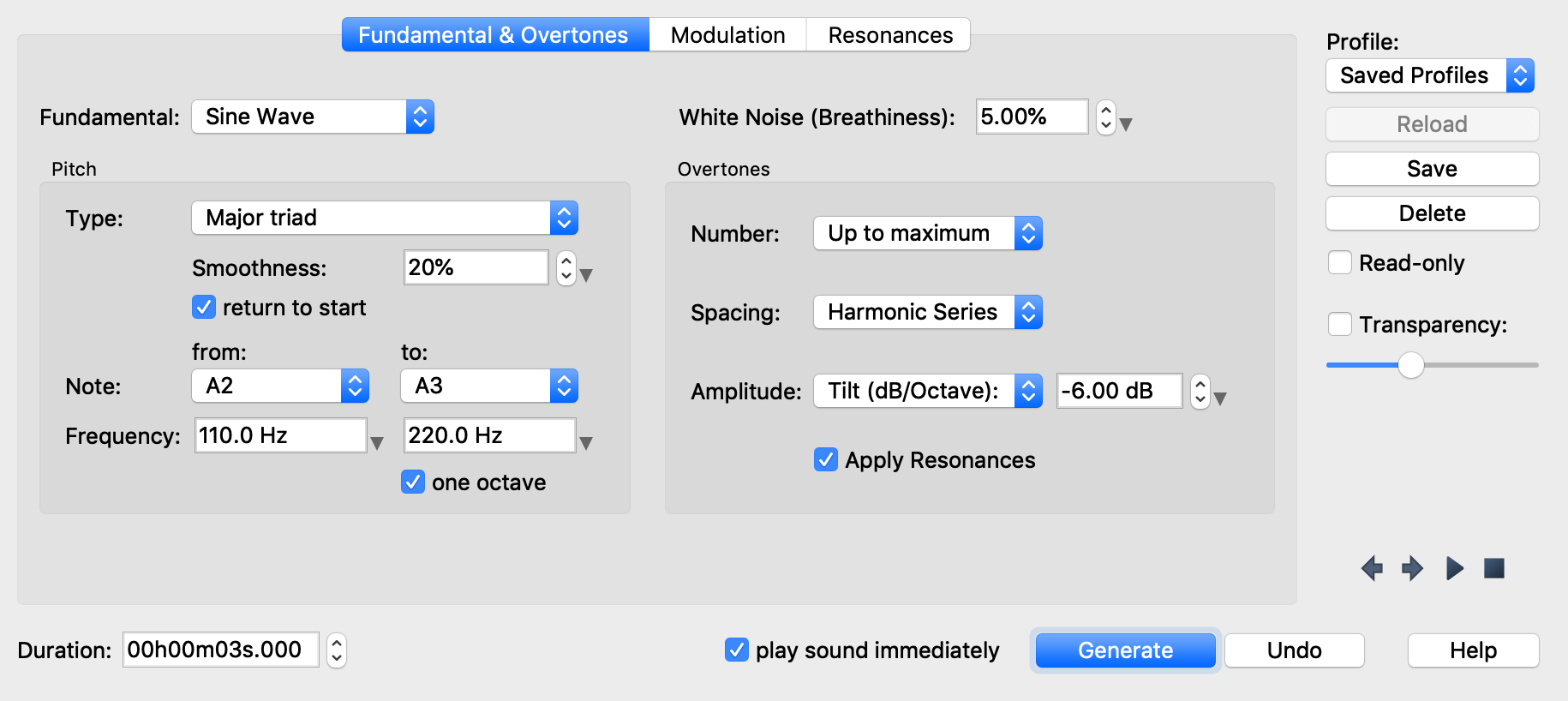
Fundamental and Overtones
The fundamental is the basic waveform from which the generated sound is composed. In can be one of the following:
- Sine Wave
Your sound will be composed of one or more sine waves added together.
- White Noise
Your sound will be pure white noise. This fundamental sound type has no additional parameters.
- Coherent Noise
Coherent Noise is somewhere between sine waves and white noise. It is a waveform that is more irregular than a sine wave, but still has a frequency.
This setting allows to mix a percentage of pure white noise to the other fundamental waveform types, which can be used to simulate the breathiness of a voice, or the background noise of a recording.
This section determines if the pitch stays constant over the duration of the sound, or if it moves, for example by forming a triad or a scale.
When the pitch type is not constant, the pitch will move from the from to the to note or frequency. You can check return to start to make the pitch move back to the starting note.
Pitch type can be one of the following:
- Constant Pitch
The pitch will be constant over the entire duration of the sound.
- Single Step
The pitch will smoothly move from the start to the finish note.
- Major / minor triad
The pitch will form a major or minor triad.
- Major / minor scale
The pitch will form a major or minor scale.
- Sweep (linear)
The pitch form a straight interpolation along the linear scale.
- Sweep (log)
The pitch form a straight interpolation along the logarithmic scale.
This section determines the number, spacing, and intensity of the overtones of the sound, which will shape its timbre.
The number of overtones can be anywhere from one (which means the sound only has the fundamental) up to the maximum that is determined by the sampling rate of the sound. In digital audio, a waveform can represent frequencies of up to half the sampling rate. For example, with a sampling rate of 44100 Hz, the highest frequency that can be represented is 22050 Hz. Therefore, overtones of up to a maximum of 22050 Hz can be included in the sound.
- Specify amount
Enter the amount of overtones. Overtones above the maximum frequency will be ignored.
- Up to maximum
Include all overtones below the maximum frequency, which is half the sampling rate.
- Up to frequency
Include all overtones below the entered frequency (or half the sampling rate, whichever is lower).
The spacing of the overtones determines the distance or the ratio between successive overtones. This allows to create sounds that are based on the natural harmonic series, as well as other sounds that have different frequency ratios between the overtones.
- Harmonic Series
Each overtone will be a whole multiple of the fundamental. For example, if the fundamental is 100 HZ, the overtones will be 200 Hz, 300 Hz, 400 Hz, 500 Hz, etc. In this case the overtones will be the harmonics of the fundamental.
- Octaves
Each overtone will have twice the frequency of its predecessor. For a fundamental of 100 Hz, the overtones will be 200 Hz, 400 Hz, 800 Hz, 1600 Hz. In this case the overtones will all be octaves of the fundamental.
- Multiply by
Each overtone will have the frequency of its predecessor multiplied by the entered factor. If the factor is 2.0, this is the same as selecting Octaves.
In mathematical terms:
frequency(n) = factor*frequency(n-1)- Fundamental factor
Each overtone will have the frequency of the fundamental, multiplied by a factor and by the number of the overtone. If the factor is 1.0, this will generate the harmonic series. In other words, the factor sets the distance between consecutive overtones.
In mathematical terms:
frequency(n) = n*factor*fundamental
This section determines the amplitude, or intensity, of successive overtones. The values are measured in decibel (dB). A value of -6 dB corresponds to a reduction of the intensity by half. If the dropoff by octave or overtone is zero, all overtones will have the same intensity. If it is negative, higher overtones will be quieter than the lower ones (this is usually the case in natural sounds).
- Tilt (dB/Octave)
The tilt sets the intensity drop per octave. With a value of -6 dB, each octave will be half the intensity of the previous octave.
- db/Overtone
This sets the intensity drop per overtone. Since the overtones follow a linear frequency scale, this setting will create a linear intensity dropoff (unlike the tilt, which will create a logarithmic dropoff).
- Half intensity / Octave
With this setting, the intensity will drop exactly in half with each octave, which is equivalent to having a tilt of -6,0206 dB per octave.
Each overtone has an intensity that is one over N, where N is the frequency of the overtone divided by the frequency of the fundamental.
In mathematical terms:
intensity(n) = 1/(frequency(n)/fundamental)